미니탭 비정규 데이터 공정능력분석

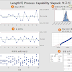
 측정된 데이터가 정규분포를 따를 때 공정능력 분석을 실시하여 보았습니다. 하지만, 모든 데이터가 정규분포를 따르지는 않습니다. 특히 데이터가 부족한 경우에 정규분포를 따르지 않는 경우가 많습니다. 공정능력분석은 관리도와 다르게 개별 데이터로 추론을 하는 방식이기 때문에, 정규성 검증이 반드시 선결되어져야 합니다. 

이번 블로그에서는 정규분포를 따르지 않는 데이터로 공정능력분석을 해보도록 하겠습니다. 정규분포를 따르는 데이터의 공정능력분석은 이전 블로그를 참조해 주시기 바랍니다.

미니탭_공정 능력 분석

데이터가 정규분포를 따르지 않는 경우 공정능력을 분석하는 방법은 크게 두 가지 방법이 있습니다.

1. 해당 데이터에 부합되는 개별 분포를 식별하고, 이 분포에 대한 공정능력 분석 절차를 사용하는 방법
2. Box-Cox 변환 혹은 Joshon 변환을 사용하여 정규 데이터로 변환한 후에 정규분포에 대한 공정 능력을 분석하는 방법

위의 두 가지 방법 중에 변환을 통하여 정규 데이터로 변환한 후에 정규분포에 대한 공정 능력을 분석하는 방법에 대해서 알아보도록 하겠습니다.

1. 정규성 검증

데이터에 대한 정규성 검정을 먼저 실시한다. 통계분석 > 기초 통계 > 정규성 검정 메뉴로 검정을 실시한다. 

① 변수에 측정 데이터를 선택한다. 

② 정규성 검정 방식을 선택하는 옵셥니다. 기존에 알아보았던 대로, Anderson-Darling 방식을 선택한다. 

정규성 검정을 실시한 결과이다. P-값이 0.006이므로 정규분포를 따르지 않는다고 할 수 있다.(P-값이 0.05보다 커야 정규분포를 따른다고 할 수 있다.)

2. 개별 분포 식별

정규 분포를 따르지 않으므로, 어떠한 분포에 적합한지를 평가해야 한다. 미니탭 메뉴에서는 통계분석 > 품질 도구 > 개별 분포 식별 메뉴를 선택한다.

① 데이터 입력 열을 선택하고, 부분군 크기를 입력한다. 이번 데이터의 경우 부분군이 없는 데이터이기 때문에 "1"을 입력한다. 데이터의 부분군이 있는 경우는 부분군 크기에 부분군의 개수를 입력하면 된다.

② 모든 분포에 대해서 검토를 할 수 있는 옵션과, 원하는 분포만 검토하는 옵션을 선택할 수 있다. 필요한 분포에 대해서만 검토할 경우 위와 같이 지정된 분포를 선택하여 적합성 검토를 할 수 있다.

적합도 검정 결과이다. Anderson-Darling 검정 값(AD)이 0에 가까우면서, P값이 유의수준 알파(통상 0.05)보다 크면서 최대 P값을 갖는 분포를 선택한다. 이 분석에서는 Jonshon 변환이 가장 적합한 것으로 나타났다. 

3. Jonshon 변환을 통한 공정 능력 분석

위의 적합도 검정을 통하여 Jonshon 변환이 가장 적합한 것으로 나타났다. 기존 데이터를 Johnson 변환하고, 그 데이터로 정규분포 공정 능력 분석을 실시하는 절차가 남았다. Johnson 변환은 Box-Cox 변환보다 내용이 복잡하나 거의 모든 경우에 적절한 변환을 찾을 수 있는 장점이 있다고 한다. 이 변환에 대한 설명은 매우 복잡하고 난해하다. 

통계분석 > 품질 도구 > 공정 능력 분석 > 정규 분포 모듈을 선택한다.

① 데이터 입력 열을 선택하고, 부분 군의 크기는 "1"이다.

② 규격 하한(USL)을 입력한다. 이 데이터의 규격은 한쪽 규격으로 하한 규격만 있는 경우로, 규격 하한을 입력한다.

③ 변환을 위해 "변환"옵션을 선택한다.

Johnson 변환을 선택하여 p-값은 기본 옵션 값 "0.1"로 둔다.

① 기존 데이터의 분포를 나타내주는 히스토그램이다. 정규분포와는 다소 다른 분포 특성이 있음을 육안으로도 확인할 수 있다.

② 기존 데이터를 변환하는 함수를 나타내준다. 이 함수를 산출하는 방법까지는 저의 한계를 벗어나는 범위라서 설명은 생략하도록 하겠습니다.

③ 변환된 데이터를 통하여 산출한 공정능력 분석 결과입니다.

변환을 통하여 공정능력을 분석하는 방법에는 두 가지 방법이 있습니다. Box-Cox 변환과 Johnson변환이 그것인대요. 두 방식에 대해서 간단히 미니탭 도움말을 보면 아래와 같습니다.

Box-Cox 변환 : 이 변환은 이해하기 쉽고 부분군 군내 및 전체 공정 능력 통계량을 모두 제공합니다.

Johnson 변환 : Johnson 변환은 매우 강력하고 0과 음수가 포함된 데이터에 사용할 수 있지만, 전체 공정 능력 통계량만 제공하는 더 복잡한 변환입니다. Johnson 변환은 Box-Cox 변환을 사용하여 적합한 변환을 찾을 수 없는 경우에 사용합니다.

지금까지 정규분포를 따르지 않는 데이터에 대한 공정능력 분석 절차에 대해서 알아보았습니다.